
Dear students, we are providing class notes on topic Slope of a Line. The concept of slope is fundamental in coordinate geometry, helping us understand the steepness and direction of a line. In Ontario’s Grade 10 Principles of Mathematics curriculum, slope is one of the first key topics covered in Chapter 1.
Slope of a Line – Definition
The slope of a line is a measure of how steep the line is. It is calculated as the ratio of the vertical change (rise) to the horizontal change (run) between two points on the line.
Formula for Slope

Types of Slopes
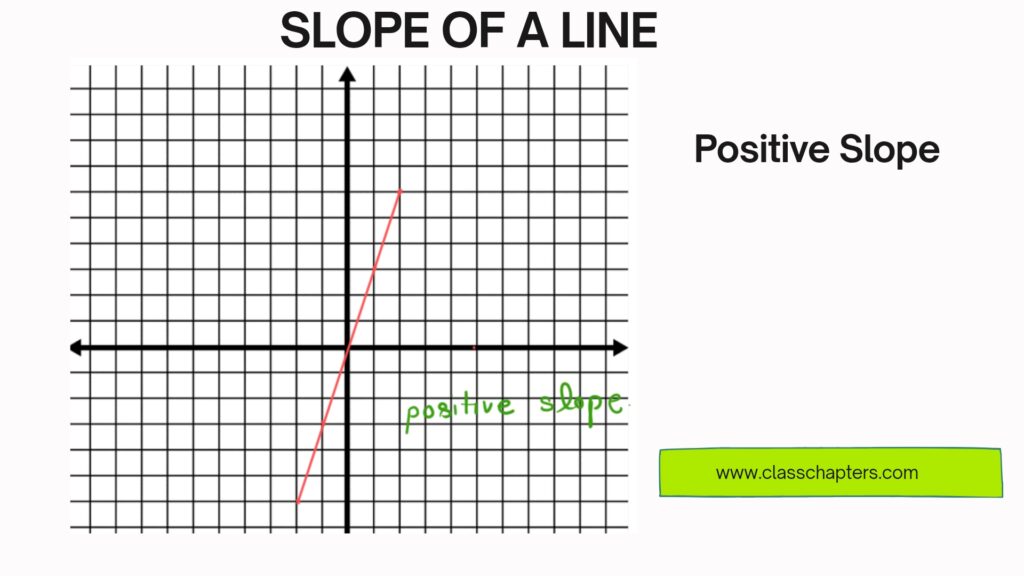
1. Positive Slope
- If a line goes upwards from left to right, it has a positive slope.
- Example: If , the line rises 3 units for every 1 unit it moves to the right.
2. Negative Slope
- If a line goes downwards from left to right, it has a negative slope.
- Example: If , the line falls 2 units for every 1 unit it moves to the right.

3. Zero Slope (Horizontal Line)
- If a line is completely horizontal, it has a slope of 0.
- Example: The equation of a horizontal line is , meaning the y-value does not change regardless of x.

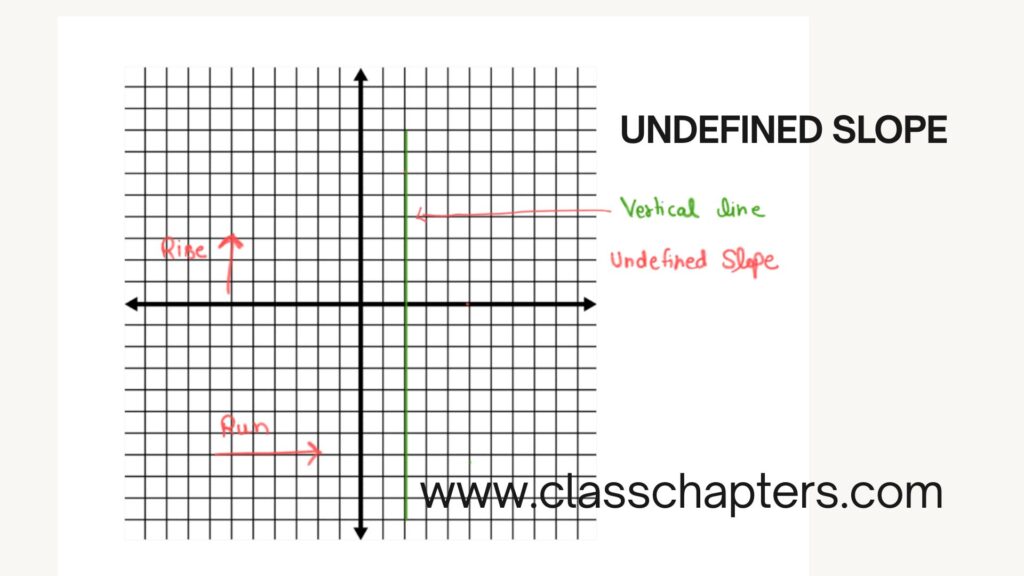
4. Undefined Slope (Vertical Line)
- If a line is completely vertical, the slope is undefined because the denominator in the formula (run) is zero.
- Example: The equation of a vertical line is , meaning the x-value does not change regardless of y.
Finding the Slope from Two Points

Example 1
Find the slope of the line passing through points A(2, 3) and B(6, 11).
Slope-Intercept Form of a Line
The most commonly used equation of a line is the slope-intercept form: y=mx+c
where:
- m is the slope.
- c is the y-intercept (the point where the line crosses the y-axis).
Example
If a line has a slope of 4 and a y-intercept of -3, its equation is:
This equation tells us that the line rises 4 units for every 1 unit it moves to the right and crosses the y-axis at -3.
Point-Slope Form of a Line
Another useful equation of a line is the point-slope form:
where is a known point on the line and is the slope.
Example
Find the equation of the line that passes through the point (3, 5) with a slope of -2.
Solution: Expanding: So, the equation of the line is y = -2x + 11.
Parallel and Perpendicular Slopes
1. Parallel Lines
Two lines are parallel if they have the same slope.
- Example: The lines and are parallel because both have a slope of 3.
2. Perpendicular Lines
Two lines are perpendicular if their slopes are negative reciprocals of each other. If the slope of one line is , the slope of a perpendicular line is .
- Example: If a line has a slope of 2, then a perpendicular line must have a slope of -1/2.
Slope in Real-World Applications
1. Road Inclines
Road slopes (gradients) are often expressed as percentages. A 10% grade means the road rises 10 meters for every 100 meters of horizontal distance.
2. Ramps and Accessibility
Wheelchair ramps must follow regulated slopes for safety. For example, in Canada, accessibility ramps typically have a slope of 1:12 (one unit of rise for every twelve units of run).
3. Roof Construction
The slope of a roof (pitch) is calculated to ensure proper water drainage. A common roof pitch is 4/12, meaning the roof rises 4 inches for every 12 inches of horizontal span.
4. Physics and Engineering
Slope calculations are crucial in physics (e.g., velocity-time graphs) and engineering (e.g., designing bridges and roads).
Practice Questions (Slope of a Line)- Click here
Online Quiz (Slope of a Line) – Click here
Principles of Mathematics (MPM2D) notes
Chapter 1 Line Segment
1.1 Distance Between Two Points – class notes click here
1.2 Midpoint – class notes click here
1.3 Slope of a Line – class notes click here
1.4 Slopes of Parallel Lines – class notes click here
1.5 Slopes of Perpendicular Lines -class notes click here
Principles of Mathematics (MPM2D) Quiz
1.1 Distance Between Two Points – quiz click here
1.2 Midpoint – quiz click here
1.3 Slope of a Line – quiz click here
1.4 Slopes of Parallel Lines – quiz click here
1.5 Slopes of Perpendicular Lines -quiz click here
