distance between two given point dear students of class 10 we are providing you the class notes for class 10 chapter 1 line segment topic distance between two given points. We can find the distance with the given coordinates and use them to compare the different geometrical figures to find the distance of line to compare the length of sides of triangles to categorized them as well as we can find the perimeter area length of a diagonal for rectangle for parallelogram. This topic is a according to class 10th Ontario syllabus for mathematics
Distance between two given points introduction
The distance between two points in a coordinate plane is a fundamental concept in geometry. It helps in calculating the length of line segments, identifying types of triangles, determining missing coordinates, and finding properties of geometric shapes such as rectangles.
Distance between two given points Formula
If two points P1(x1,y1)P_1(x_1, y_1)P1(x1,y1) and P2(x2,y2)P_2(x_2, y_2)P2(x2,y2) are given, the distance between them is calculated using the following formula

Thus, the distance between the two points is 5 units.
Identifying Triangle Type with Given 3 Vertices
Given three points A(x1,y1)A(x_1, y_1)A(x1,y1), B(x2,y2)B(x_2, y_2)B(x2,y2), and C(x3,y3)C(x_3, y_3)C(x3,y3), the type of triangle formed can be determined using the distance formula for all three sides:
- If all three sides are equal, the triangle is equilateral.
- If only two sides are equal, the triangle is isosceles.
- If the sum of squares of two sides equals the square of the third side, the triangle is right-angled (Pythagorean Theorem).

3. Finding a Missing Coordinate When Distance is Given
If one coordinate is missing and the distance is provided, we use the distance formula to solve for the missing value.
Example 3: Find k if the distance between (k,3) and (4,7) is 5.
Using the formula:Using the formula:

4. Finding Perimeter, Area, and Diagonal of a Rectangle
A rectangle has opposite sides equal. Given the four vertices of a rectangle, we can:
- Find the side lengths using the distance formula.
- Compute the perimeter: P=2(length+width)P = 2({length} + {width})
- P=2(length+width)
- Compute the area: A=length×Width = {length} {width}=length×width
- Find the diagonal using the distance formula.

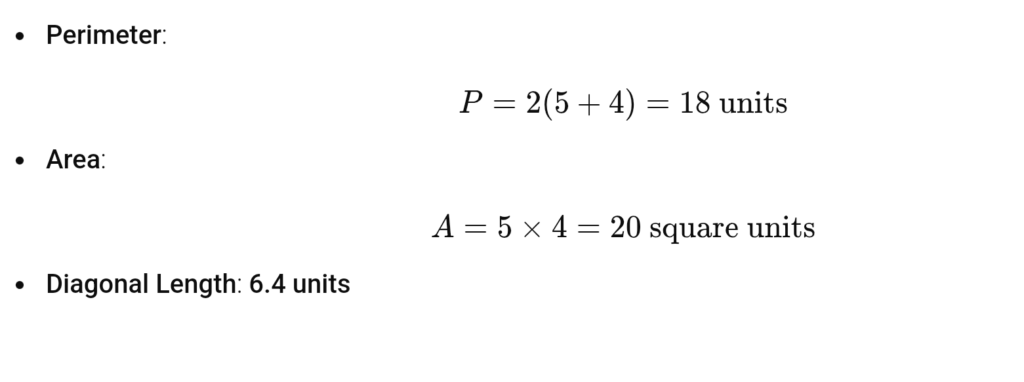
Practice Questions (Distance Formula)- Click here
Online Quiz (Distance Formula) – Click here
Conclusion
So this block will help you to understand the following concept
- The distance formula helps measure the distance between two points.
- Given three vertices, we can classify the type of triangle based on side lengths.
- If the distance and one coordinate are known, we can find the missing coordinate.
- We can use distances to compute the perimeter, area, and diagonal of rectangles.
Other links
Principles of Mathematics (MPM2D) notes
Chapter 1 Line Segment
1.1 Distance Between Two Points – class notes click here
1.2 Midpoint – class notes click here
1.3 Slope of a Line – class notes click here
1.4 Slopes of Parallel Lines – class notes click here
1.5 Slopes of Perpendicular Lines -class notes click here
Principles of Mathematics (MPM2D) Quiz
1.1 Distance Between Two Points – quiz click here
1.2 Midpoint – quiz click here
1.3 Slope of a Line – quiz click here
1.4 Slopes of Parallel Lines – quiz click here
1.5 Slopes of Perpendicular Lines -quiz click here

